A középértékek publikálásával kapcsolatban mindig eszembe jut, hogy a középértékek számítása hogyan változtathatja meg a perspektívát. Mivel gyakran használjuk a középértékeket stratégiák tesztelésére, eredmények értékelésére és gazdasági adatok elemzésére, fontos megérteni, hogy ezek a számítások gyakorlati pénzügyi alkalmazásokban korlátozottak lehetnek. Cikkünk célja, hogy bemutassuk a medián számítás és a középérték közötti különbségeket, valamint azt, hogy mikor érdemes őket figyelembe venni.

Miért Lehet Megtévesztő a Középérték?
Aritmetikai középérték (más néven átlag) kiszámításához összeadjuk az adatokat, majd elosztjuk a darabszámmal. Például az (1, 10, 4, 8, 10, 5) adat sorozat aritmetikai középértékét így számíthatjuk ki:
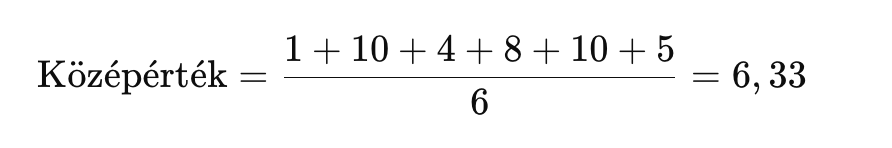
Bár a számítás egyszerű, problémák merülhetnek fel, amikor a középértéket próbáljuk az adatsor tipikus értékeként értelmezni. Például, ha az egyik adatot 500-ra módosítjuk, a középérték jelentősen, 88,8-ra emelkedik. Ez azt jelzi, hogy a szélsőséges értékek torzíthatják a középértéket, és nem mindig tükrözik a többségi adatokat.
Ezért fontos a medián figyelembevételével is megvizsgálni az adatokat. A medián az adatsor középső értéke, ha az adatokat növekvő sorrendbe rendezzük. Ha az adatok száma páratlan, a medián az adatsor középső értéke. Ha páros, a medián a két középső érték átlaga.

Az első esetben a középérték és a medián közötti különbség nem jelentős, míg a második esetben a középérték (88,8) és a medián (9) közötti eltérés jelentős, ami az adatok szélsőséges eltérésére utal.
Hogyan Számítjuk Ki a Mediánt és a Képletét
A medián pontosabb képet ad az adatok középső értékéről, különösen, ha az adatok szélsőséges értékeket tartalmaznak. A medián számítása a következő lépésekből áll:
- Rendezzük az adatokat növekvő sorrendbe.
- Ha az adatok száma páratlan, a medián az adatsor középső értéke. Ha páros, a medián a két középső érték átlaga.
Hogyan Tisztázzuk a Középérték Számítását?
Aranyhu.com – Az adatelemzés során a középértékeket gyakran kiegészítjük a szórás mértékével, amely megmutatja, mennyire variálódnak az adatok a középértéktől. A szórás azt méri, hogy az adatok mennyire térnek el a középértéktől. A szórás képlete:
Szórás = √((Σ (Xi – X̄)2) / n)
Ahol:
- Xi az adatminták elemei,
- X̄ a minták középértéke,
- n az adatminták száma.
Példa:
Tekintsük az (1, 4, 5, 8, 10, 10) adatokat, ahol a középérték 6,33:
- Számoljuk ki az eltéréseket a középértéktől:
- 1 – 6,33 = -5,33
- 4 – 6,33 = -2,33
- 5 – 6,33 = -1,33
- 8 – 6,33 = 1,67
- 10 – 6,33 = 3,67
- 10 – 6,33 = 3,67
- Négyzetre emeljük az eltéréseket:
- (-5,33)2 = 28,41
- (-2,33)2 = 5,43
- (-1,33)2 = 1,77
- 1,672 = 2,79
- 3,672 = 13,47
- 3,672 = 13,47
- Az eltérések négyzetre emelt értékeinek összege:
- 28,41 + 5,43 + 1,77 + 2,79 + 13,47 + 13,47 = 65,44
- Számoljuk ki a szórást:
- Szórás = √(65,44 / 6) = √10,91 ≈ 3,30
A szórás segít megérteni, hogy mennyire pontosan tükrözi a középérték az adatokat. Magas szórás azt jelzi, hogy az adatok jelentősen eltérnek a középértéktől.
Milyen Problémák Merülhetnek Fel a Középértékű Befektetési Hozamokkal Kapcsolatban?
Medián Számítás és Átlag – A középértékekkel kapcsolatos problémák a befektetési hozamok esetében is jelentkezhetnek. A változékony hozamok esetén a középérték nem mindig tükrözi pontosan a befektetés teljesítményét. Például:
- Az első évben 100%-os hozam, a befektetés HUF 1 millióról HUF 2 millióra emelkedik.
- A második évben -50%-os hozam, a befektetés HUF 2 millióról HUF 1 millióra csökken.
Bár a középérték 25% lehet, a befektetés tényleges növekedése nem változott, így a középérték megtévesztő lehet.
CAGR (Kibővített Éves Növekedési Ráta) Számítása és Értelmezése
A CAGR a Compound Annual Growth Rate, azaz Kibővített Éves Növekedési Ráta rövidítése. Az egyszerű számítás ellenére a CAGR pontosan tükrözi a teljes időszak alatt az éves növekedési ütemet. A képlet:
CAGR = (Vf / Vi)1/n – 1
Ahol:
- Vf a végső érték
- Vi a kezdeti érték
- n az évek száma
Példa:
Ha HUF 1 milliót fektetünk be, és a harmadik év végére HUF 1,2 millióra nő, akkor a CAGR 6,27% lesz. Ez pontosabb képet ad a teljesítményről, mint a középérték.
Összefoglalva, a középérték, különösen magas kockázatú eszközök esetén, megtévesztő lehet. A befektetések teljesítményének pontos értékeléséhez ajánlott a CAGR-t használni, mivel egyszerűen kiszámítható és pontosabb képet ad a befektetések növekedéséről.
Összefoglaló
A középértékek gyakori használata a pénzügyi elemzésekben és stratégiák tesztelésében fontos, de tisztában kell lennünk azok korlátaival. A középérték, bár egyszerűen számítható, gyakran torzíthatja az adatokat, különösen, ha szélsőséges értékek vannak jelen. Ilyen esetekben a medián, amely az adatsor középső értékét jelenti, pontosabb képet adhat az adatok eloszlásáról. A medián előnyös lehet az adatok szélsőséges eltéréseinek kezelésében.
A középértékek mellett fontos a szórás figyelembe vétele is, amely megmutatja, hogy az adatok mennyire térnek el a középértéktől. A magas szórás arra utalhat, hogy az adatok jelentősen eltérnek a középértéktől, és így az nem mindig tükrözi pontosan az adatokat.
A befektetési hozamok esetében a középértékek szintén problémásak lehetnek, mivel nem mindig tükrözik a befektetések tényleges teljesítményét. A CAGR (Kibővített Éves Növekedési Ráta) használata pontosabb képet adhat az éves növekedési ütemről, mivel figyelembe veszi az időbeli változásokat.
Összességében, a középértékek korlátainak felismerése és a medián, valamint a CAGR használata segíthet a pénzügyi elemzések pontosabb értékelésében.





